This is the video of a talk I gave at the British Logic Colloquium, on the topic of “Random Graphs in Logic and Network Science”, attempting to make some initial connections between two very different ways of thinking about random graphs.
It’s a primary school homework question which causes disagreement among seasoned mathematicians. In order to find the correct answer, I called upon that most rigorous of scientific instruments, the Twitter poll:
In retrospect I regret not including a “none of the above” option, but more on that later. In this post I’m going to go through these three answers (and “None of the above”), and discuss their pros and cons as I see them, before dramatically revealing the correct response.
But first: why can’t we straightforwardly give the right answer? The words in the question are hardly mysterious. We all know what a “circle” is, what it means to count “how many” of something, and what a “side” is… or don’t we? Here are (rough) definitions I distilled from discussions with two primary school students who had been on the receiving end of this question:
1. A line forming part of a shape’s boundary of a plane figure.
The purpose of saying plane figure rather than “shape” here is that we want shapes that live in 2-dimensions (e.g. squares or circles, but not spheres or cubes). The next question is what a “line” is in definition 1. Here’s a variant which pins that down:
2. A straight line forming part of the boundary of a plane figure.
If you type “define: side” into Google, the most relevant definition is:
“a minibus was parked at the side of the road”
antonyms: centre, heart, end
“the farm buildings formed three sides of a square”
A rectilinear figure is one constructed from straight lines. So this definition is a further refinement of definition 2, and allows us to affirm that a square has four sides, but on the face of it has nothing to say about non-rectilinear plane figures such as circles.
Infinitely Many Sides?
I think it’s a safe bet that the respondants to my Twitter poll have a higher level of mathematical education than the national average. The fact that they were split on this question at all, and that a small majority selected an answer which is pretty well unavailable to this question’s usual audience (primary school students), certainly suggests something going wrong somewhere.
So, does a circle have infinitely many sides? It is definitely useful to consider a circle as the limit of n–sided polygons as n gets bigger and bigger. This is exactly the approach that Archimedes, Liu Hui, and countless others have used down the centuries to study circular geometry, including coming up with approximations for π.

A 16th century Ming dynasty edition of the Jiuzhang suanshu (Nine Chapters on the Mathematical Art), third century CE.
Sometimes it is absolutely sensible, as a convenient shorthand, to think of a circle as being like a polygon with infinitely many sides.
But, as an insufferable pedant a mathematician, I’d want to distinguish between convenient shorthand and literal truth. If we’re adamant that a circle really is a polygon with infinitely many sides, then the question presents itself: what are the sides? And surely the only plausible answer[1] is: the individual points of the circle. How long are these so-called sides? Zero centimetres. And are these sides separated by corners? Not apparently, either there are no corners at all, or every point is both a side and a corner.
I’d say sides of length zero are… a problematic concept. How can you tell whether you have got any? For instance, suppose I’m studying a system where a square arises as a limit of octagons like this:

In this situation, it might well make sense for me to think of my square as having eight sides, four of which have length zero. But if I was to insist that my (perfectly ordinary) square really does have eight sides, you might raise an eyebrow.
So this – the winning answer in my poll – is the only one I am going to declare to be definitively wrong, while it is also the only one which offers any geometrical insight at all. A paradox? Not really. Reasoning by analogy is a valuable skill in mathematics and in life; at the same time it is important to hold on to the realisation that that is what we are doing.
For infinitely many sides: geometrically illuminating.
Against infinitely many sides: eight-sided squares.
Off on a tangent 1: apeirogons
Even if a circle isn’t one, are there such things as polygons with infinitely many sides? Well, there is a word to describe such a thing an apeirogon. A regular apeirogon would then have sides of equal (non-zero) length with equal angles between them. The only option here is this stupendously unexciting object:
![]()
If you object to this as being a “polygon” (either bcause of the angles of 180° or the chain of edges not closing in a loop), how about something like this: start at the bottom of a circle, and at each stage move around half of what remains of the circle, and replace the arc you’ve just travelled with a straight edge:
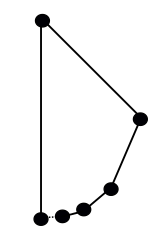
Is this a genuine polygon? Once again it depends on your terms. According to one common definition, that of a “closed polygonal chain”, this fails to qualify since the starting corner (bottom left) only connects to one edge. But it’s a very near miss: that point is the limit of a sequence of edges from the right, making this shape a “non-self-intersecting piecewise linear closed curve”, another definition of polygon that people use.
If we leave our usual Euclidean world and enter hyperbolic space, then there is no ambiguity. Apeirogons (even regular apeirogons) simply exist:
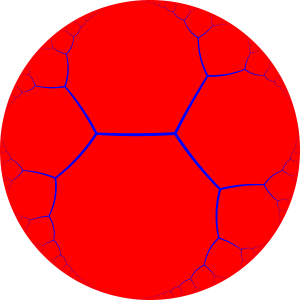
A tiling of the hyperbolic plane by regular apeirogons. (By Anton Sherwood – Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )
Off on a tangent 2: extreme points
It might be more defensible to say that a circle has infinitely many corners than infinitely many sides (although this is not a question that seems to get asked very often). To start with, if a corner of a square is a point at which its boundary line is not straight, then every point on the circle satisfies that. More sophisticatedly, there is a notion of an extreme point of a shape: that is any point through which you can draw a segment of straight line which touches the shape only at that exact point. For a square and many familiar shapes the extreme points exactly coincide with the corners. Every point on the boundary of the circle is an extreme point, so it is certainly true that a circle has infinitely many.
We might worry that some shapes such as this chevron have corners which are not extreme points:

Here the lower central corner is not an extreme point (the other three corners are). What’s going wrong is that this shape is not convex (roughly, it has some bits sticking out too far). A circle is convex, so perhaps we needn’t worry. Alternatively, we might remedy the situation by defining a “corner” to be a point which is an extreme point either of the shape in question or of its complement, i.e. the whole plane with the shape cut out of it. That approach would detect corners of all polygons, including the chevron. For smooth curves, it would identify all boundary points as “corners” except for inflection points (which is not unreasonable since we might argue that the boundary is straight there).
One Side?
In primary school, it seems that “one” is the answer that gets the tick. And there is a moderately decent justification. Remember definition 1 above:
1. A line forming part of the boundary of a plane figure.
The immediate question is what counts as a “line”, especially if we are not insisting on straightness. If we are too relaxed about this, then any plane figure could be said to have “one side”, in the same sense that it has one boundary, perimeter, or circumference. But this has got to be wrong, as we surely want a square to have four. Well, a square has four points where it is not smooth, with four smooth sections in between. Perhaps it was really the smooth sections that we were counting all along. So implicitly we have a new refinement of definition 1 (and also take the opportunity to ditch the vague term “figure”):
4. Each smooth section of a piecewise-smooth closed curve.
A “closed curve” is one which loops around to meet itself so that it has no free ends. “Piecewise-smooth” means that it is built from smooth sections, which meet at isolated unsmooth points. It is perfectly legitimate to want to count the smooth sections of such a shape’s boundary, and it’s by no means outrageous to use the word “side” when doing that. So I’m certainly not saying this is definitively the wrong answer.
The question is whether that interpretation of “side” is not merely coherent, but natural enough that it can simply be presumed without being stated explicitly (which it seldom if ever is). What happens when smoothness and straightness tally up differently? Consider this tombstone shape, created by replacing the top of a square with a semicircle of equal diameter.
This has two smooth sections (the bottom line and the rest) but three straight edges (plus a curved piece smoothly[2] joining two of them). So how many sides does it have? I consulted my Twitter friends again:
This time I should have included “infinitely many” as an option, although that can be absorbed into “None of the above”. Anyone voting that the circle has infinitely many sides should automatically vote “None of the above” here, unless – an important caveat – the nature of this shape indicates to the reader a different notion of “side”. The fact that the most popular choices in these two polls are incompatible suggests this may be the case (or at least reinforces that the waters are muddy).
Although two is a perfectly respectable answer, compatible with definition 4 above and with a circle’s one-sidedness, I am not satisfied it is definitively the right one, or that three or four are categorically wrong. It depends what you want to count: smooth sections, straight edges, or straight edges plus whatever’s then leftover, any of which might be the answer you want depending on context (more on this below). Relatedly, I am not sure counting the number of smooth sections fully matches my intuition of the word “side”. After all, the tombstone’s two upright sections are – I think it is fair to say – “on opposite sides”. Are we really content that they are simultaneously part of the “same side”?[3]
You might protest that I am conflating two different meanings of “side”, that terminology sometimes clashes, and we just have to live with it. I am not so sure, though. The point of this exercise is to extrapolate from a situation (rectilinear figures) where the two notions mesh pretty well. If there was a new idea which captured everything we liked about the original but also applied to a broader category of shapes, then that would have an overwhelming claim to being the unique right answer. But if all our attempts at generalisation involve sacrificing desirable aspects of the original, then perhaps there is no single correct generalisation. There are different choices, with different trade-offs, which might be suitable in different contexts (and if we’re in a situation where more than one are in play, then they could helpfully be given different names).
Here’s a another variation: a Weierstrass tombstone created by replacing the top edge of a square by a section of Weiestress function, an infinitely wiggly line which isn’t smooth anywhere.

Here (and spot the typo) is what my Twitter friends made of this – although fewer ventured an opinion:
Notwithstanding the scepticism of my Twitter followers, I’ll explain in a minute why I don’t think it’s silly to see this as having four sides (one of which is non-smooth). On the other hand, if you prefer your sides smooth, then you again have a choice between seeing it has having infinitely many sides (three of which have length 1, and the rest having length 0), or having 3 sides plus a stretch of definitely-not-a-side boundary.
For one side: a single smooth curve.
Against one side: the same side on opposite sides.
Off on a tangent 3: sides versus edges
How many sides does a square have? Four. How many edges does it have? Four. So are edges and sides the same thing? Not necessarily. Here are two configurations which are – at least arguably – each four-sided but have 5 and 3 edges respectively:
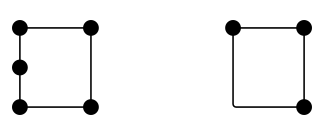
Usually, I would say, an “edge” is a topological object, in that its function, not its shape, is what matters. Think of the London tube map. If you asked how many edges there are in that network, there’s no merit in totting up straight or smooth sections. It’s connections between stations (or vertices) that count.
As already mentioned, it’s common to think of a polygon as a very simple sort of network called a closed polygonal chain: a string of vertices (in this case the corners of the polygon), linked with edges, in such a way that every vertex lies on exactly two edges, and the whole thing forms a single loop. In this situation edges and sides coincide, as do vertices and corners. But in general you can break this concurrence, as in the two small networks above.
If you want to think about things network-theoretically, but the vertices aren’t clearly marked, then you have to guess where they are. With a polygon this is easy – the vertices are at the corners – which is why switching between geometric and topological approaches comes so naturally. But with other shapes, such as either of the tombstones above, it may not be so obvious. Nevertheless, in each case if you were told there were vertices in there somewhere, and were asked to locate them, I think it would be sensible[4] to guess that there are four, namely the corners of the original square, and that the top edge has for some reason been represented as a non-straight line. And if we do want to think about things that way, with each of the tombstones having 4 edges, then it might seem peverse (although logically coherent!) to insist that they have some other number of sides (especially as the top side is – despite its own geometry – clearly “on one side” of the figure). In fact, rather than guessing, one of my Twitter correspondents asked me “Have both top vertices been removed?”, a question which only makes sense from a network-theoretic perspective.
Where does this leave the circle? The trouble is that no point on the circle has a better claim to be vertex than any other. So although it is tempting (and again coherent) to view a circle as a network with one edge, if we are going to insert vertices, there is no obvious reason to prefer one to any other number.
Could we view it as a network with no vertices at all, a sort of Tube line with no stations? The usual mathematical conception of a network would not allow that, but that shouldn’t deter us too much. This suggests a purely topological approach. The trouble is that from that point of view, while a circle may be a sort of network with no vertices and one edge, so too is a square (if that’s how the Tube line happens to be laid out). In topology, a square is a circle. (This is not a paradox, it is simply saying that the boundary is a single loop, whose shape doesn’t matter.) So while this sort of network has “one edge”, obviously a square does not have “one side”, so the relationship between sides (geometric) and edges (topological) has again broken down, just as it does in the two little networks pictured above. So this appoach doesn’t take us very far forward.
No Sides?
It might seem paradoxical to argue that a circle (or any shape) has “no sides”. But the argument for the defence is straightforward. We return to definition 2:
2. A straight line forming part of the boundary of a plane figure.
This is a simple, easily understandable phrase that perfectly captures the sides of a square. We have failed to find a satisfactory generalisation of this to curved figures, so the best thing to do is stick with the original. And a circle doesn’t have any.
For no sides: true, according to a sensible notion of “side”.
Against no sides: sounds like a Zen koan.
None of the Above?
Recall the definition supplied by Google:
3. Each of the lines forming the boundary of a plane rectilinear figure.
Attempting to apply this to a circle – a non-rectilinear figure – produces nothing. The question is as meaningless as “How many sides does Monday have?”
Since Definition 3 is the most official (the only one in this post not made up by me or my children), doesn’t that make “None of the Above” categorically the right answer? Maybe. On the other hand: when someone poses us a question, the principle of charity perhaps requires us to assume that it is meaningful unless we can firmly establish otherwise, and definitions 1, 2, 4 and other variants make that possible. Further, definition 3 is linguistic rather than formally mathematical, and is therefore descriptive rather than prescriptive, so we should not be hidebound by it.
For none of the above: semantic malfunction.
Against none of the above: dialogic charity.
The Right Answer
What prompted me to write this post? Like countless primary school students, my five-year-old twin sons – the primary school students mentioned at the start – were recently asked this question in their homework. One plumped for “1” and the other “0”, and I have tried to capture and expand on their reasoning above. I think both answers are wholly defensible – and neither is definitively right.
So, what should you do if you’re asked the question: How many sides does a circle have? In my opinion, the optimal response is to approach the mathematician in your life to write a 3000 word treatise on the topic, which you can then print out and triumphantly deliver to your unfortunate teacher. But failing that, the best approach is to follow the example of Socrates and respond to the question with a counter-question: What do you mean by “side”?
When all’s said and done, counting up to zero, or to one, or refusing to answer the question, tells us virtually nothing about the geometry of circles. But there is a lot to be gained by teasing apart familiar notions, dropping or adding extra conditions, challenging our intution by moving from one context to a slightly different one, and trying to write down precisely what we mean by a particular term in a particular setting. That’s what real mathematics is all about.
Footnotes
[1] You could do something else: e.g. pick a starting point P on the circle, from which to measure distance around the circumference. Then declare that the points a rational distance from P are corners and rest are sides. This has effect of yielding a countably infinite number of corners and an uncountably infinite number of sides. Or one could stipulate the opposite. This might be a convenient fit for the polygonal limit approach to circles, but I’d struggle to agree that it’s easy or obvious enough to be considered “the right answer”.
[2] One of my Twitter correspondents was worried about how smooth the curve is. This tombstone is continuously differentiable but not twice so. It would certainly be interesting if many people thought this was a critical matter, and this could probably be tested with an infinitely smooth tombstone built from something like this, although I haven’t thought through the details.
[3] We might try to formalise this as follows: in a square (or any polygon), a side has the property that starting from any position in the interior, you can cut the shape straight through your location, so that your chosen side is firmly on one side of the cut. That doesn’t work for the two-sided tombstone: any cut will always sever the long side. We could weaken this by saying that to count as a side, there has to be at least one way of slicing through the shape so that the side is on one side of the cut. That would allow us to say that the tombstone has four sides (even though the curved section is not on one side of points in the upper region). For the circle though, its supposed one side is never on one side (so would be ruled out), and only the straight section of a semicircle would count as a side.
[4] It’s not easy to come up with a rigorous justification that works for both tombstones, but I am thinking more informally in terms of Schelling Points: that is to say locations which stand out as being special for reasons which may not be easy to predict in advance.
Acknowledgements
Thanks to everyone who participated in or retweeted my polls, or discussed this with me on Twitter.
[This is a sequel to my previous post Magforming the Johnson Solids. Please see that for a disclaimer and (if you want to understand the words in this post) the geometrical background. If you only want to see some pretty pictures, then ignore all this stuff and just scroll down…]
Last time, we investigated the shapes that can be built out of regular polygons, focusing on convex shapes – roughly speaking those with no holes, dents, or spikes. There are exactly 98 theoretically magformable convex polyhedra: all 5 of the Platonic solids, 11 Archimedean solids (out of 13 in total), 4 prisms (of an infinite family), 4 antiprisms (ditto), and 74 Johnson solids (out of 92).

Once you drop the requirement for convexity, the only limits are your imagination and the size of your magformer collection. In principle there are inifinitely many magformable polyhedra, because you can always stick more bits on. See robopenguin here, for example.
So what to do? Let’s return to the starting point of every discussion of polyhedra: the Platonic Solids.
[Disclaimer: this is not a sponsored post or advert – it is a product purely of my own enthusiasm. But in the interests of full transparency, let me say one thing: for reasons you may come to understand, I developed a deep desire for some Magformers octagons. Although these exist, they are like gold-dust. So I wrote to Magformers UK and asked whether they might sell me six octagons as a special deal, and they very generously replied that they would give me six octagons, which indeed they did, for which I am eternally grateful, and which you can spot in some of the photos below. They feature more prominently in the follow-up post which is [update] here.]

The Platonic solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
When some kind soul gave my children a set of Magformers – a magnetic construction toy mainly comprising regular polygons – needless to say the first thing I did was steal them for myself and set about building up the collection until I could create the five Platonic solids.
The next shapes to move on to are the Archimedean solids. There are 13, of which 10 are realistically buildable (the truncated dodecahedron and truncated icosidodecahedron require decagons which Magformers don’t (yet?) make, and the snub dodecahedron requires unfeasibly many triangles (80) and would in any case collapse under its own weight). Here’s a sample of three:

A cuboctahedron, rhombicuboctahedron, and truncated icosahedron.
It’s been a long time since I posted anything here… and that doesn’t change now, except in a technical sense. My writing activities are currently split between my work for the European Mathematical Society (see here for why you should join) and writing about the current political situation, with which I am greviously displeased, on social media. If you are interested in the latter, see my Twitter account on your right, and I have also started a blog on Medium. The first post is: Remaining Angry.
Imagine the benefits that could reaped if economic activity could be organised in a rational and scientific way, instead of abandoned to the chaos the marketplace! Imagine the efficiency gains there would be, with workers, managers, farms, and factories all pulling together instead of wastefully competing against each other!
For a period, in the Soviet Union of the 1950s and 60s, there was a genuine and exhilarating belief not just that communism was morally preferable to capitalism, but that it could actually beat capitalism at its own game. There was even a moment, at least for those with the eyes to see it, when it looked as if that might just be beginning to happen.
It is this era which is so brilliantly captured in Francis Spufford’s fictionalised account, Red Plenty. I was recommended the book by the estimable Miranda Mowbray, when we were both speakers at a maths outreach day in London. Her talk was on “Drinking from the fire hose – data science”. Mine was on Linear Programming, and afterwards Miranda remarked that she’d read a book in which Linear Programming was the main character. And so it is.
For the question arises: in the absence of a market to balance supply and demand, how should the central planners set about their work? How much viscose should they instruct a particular factory to produce, given the number and locations of other factories, the availability of sulphur, salt and coal, and the requirements of the fabric, cellophane, and tyre manufacturers?
Astonishingly, the mathematician Leonid Vitalevich Kantorovich was able to devise a tool to answer to this sort of conundrum, in his seminal 1939 work on optimal resource allocation. (It would earn him a Nobel Memorial Prize in Economics in 1975.) The consequence of this breakthrough was spectacular: the political apparatus of central planning could be armed with linear programming, the technical means to accomplish that task, and thus would usher in a new era of Soviet abundance.
Well, it’s hardly a spoiler to say that it didn’t work out quite like that. Red Plenty recounts the rise and fall of that tide: from the elation of discovery and the hope of a better world, to frustration, cynicism, and the ultimate tragedy of failure.
Now, a book about a doomed political philosophy and a technical mathematical procedure may be admirable, but is it entertaining? Reader, it is rip-roaringly so. The story is told episodically, each chapter built around one character, sometimes real, sometimes fictional, each passage invested with the significance that its inhabitants feel. Some are hilarious, some horrifying.
There is Kantorovich, of course, the prodigy and professor. There is the ambitious but sincere (fictional) young economist Emil Shaidullin, trudging through fields in his best city suit, determined to improve the lot of the rural poor. Sasha Galich is a (real) flamboyant song-writer and playwright, becoming uneasy with the ends to which his art is put. Zoya Vaynshteyn is a (fictional) scientist enjoying a mad midsummer’s night, but quietly pitied by her colleagues for the unsayable truth: that her subject, genetics, is afflicted with the plague of Lysenkoism. Sergei Lebedev is a (real) computer pioneer, toiling away in his Institute’s basement to build the machines that will perform the enormous economic calculations far faster than any capitalist market. We meet Mr Chairman, Nikita Sergeyevich Khrushchev himself, travelling to the USA to strike a deal and issue oafish challenges. A (fictional) central planner Maksim Maksimovich Mokhov juggles the balances for 373 commodities in the chemical and rubber goods sector.
What’s so compelling is the colour and humanity of all these people as they live their lives entangled in the Soviet system. Some embrace the socialist dream, some resist, many simply try to organise their affairs around it. There are a few striking characters we meet only once, such as the (fictional) wheeler-dealer Chekuskin, frantically digging his clients (and himself) out of political holes in the Urals. But several we revisit at later stages of their careers, when dreams have died (or been revised downwards), consciences have been pricked, or lines have finally been crossed. Whilst an idea, that of Linear Programming, may indeed be the story’s main character, it is the human supporting cast that makes it so engrossing.
As a postscript, it is worth stressing that Linear Programming really did change the world, and in an altogether more desirable fashion than can be said for the command economy. As so often during the Cold War, very similar work was carried out independently and in parallel on opposite sides of the Atlantic. Linear Programming arrived in the USA with George Dantzig’s 1947 discovery of the Simplex Algorithm. Nowadays, these techniques are employed daily by countless organisations around the world to solve otherwise intractable optimisation problems.
Barry Cooper, who very sadly died on Monday, was a central member of the Leeds logic group since the 1960s. I joined that group as a graduate student in 2001, and since then have had the pleasure to get to know him. He always took an active interest in his younger colleagues, mysel f included, and was enthusiastic about mathematical outreach. Of all the senior mathematicians at Leeds, I would say Barry was the most vocally supportive of my early efforts in that area, and I remain grateful for his support.
f included, and was enthusiastic about mathematical outreach. Of all the senior mathematicians at Leeds, I would say Barry was the most vocally supportive of my early efforts in that area, and I remain grateful for his support.
Barry’s research interests were in the field of computability (or more accurately incomputability) and in particular the structure the Turing degrees. Roughly speaking, a set of whole numbers X has a higher Turing degree than another (Y) if a computer with access to X has the power to tell which numbers are and are not in Y. Thus, in a very natural sense, X contains all the information that Y does (and possibly more). It may be that Y can do the same for X, in which case the two sets have the same Turing degree.
This simple idea produces a fascinating and fundamental structure, known to the experts as the upper-semi-lattice of Turing degrees. There are all kinds of weird and wonderful configurations hiding within it: two degrees where neither is higher than the other, individual degrees which are minimal (in that there is nothing below them besides the zero degree of computable sets), two degrees which have no greatest lower bound (this is what makes it a semi-lattice rather than a full lattice), and a great deal else besides. This structure (and assorted close relatives) has been the subject of a huge amount of investigation. Barry has played a leading role in this programme over many years.
Outside research mathematics, Barry was popular, active, and successful in a frankly alarming number of different arenas. He was an excellent and well-liked teacher, and will surely be missed by Leeds undergraduate mathematicians as well as by his colleagues and numerous current and former graduate students.
In sport, he was a keen long-distance runner, with a personal best marathon time of 2hrs 48mins. His most recent outing was the 2010 London marathon. One common interest he and I shared was jazz, with Barry having a particular taste for its wilder and more avante garde varieties. He was a founder of Leeds Jazz, and helped attract numerous top artists to the city, including Art Blakey, Courtney Pine, Paul Motian, and Loose Tubes (to pick 4 examples just from 1986). One regret I have is not going to more gigs with him.
A committed political activist and unapologetic left-winger, Barry was involved in various political campaigns, including the the Chile Solidarity Campaign that was set up following the military coup of 1973.
In recent years, Barry devoted a huge amount of energy to the Alan Turing centenary events of 2012. An utter triumph, this anniversary had an astonishing global impact (and overflowed enormously beyond its allotted twelve months), and made great progress in bringing Turing the long overdue recognition he deserves. One outcome of the year was the book Alan Turing: His Work and Impact, edited by Barry and Jan van Leeuwen, a hefty and definitive volume which scooped several prizes, including the Association of American Publishers’ R.R. Hawkins Award. Another result of the increased publicity was a Royal pardon for Turing in 2013; another was the Imitation Game film of 2014. The success of the whole project was in large part due to Barry’s leadership, and the mathematical and computer science communities surely owe him a large debt of gratitude.
Barry announced just two weeks ago that he had been diagnosed with untreatable cancer, a development he met with a characteristic selflessness and equanimity. He died on Monday, surrounded by his family. Over the course of his life, Barry touched many people in many ways, and just as many will now miss him.
Yesterday, my twin sons turned one. I have spent an amazing number of hours over the last year watching them. I wondered if this experience might teach me something too, about how to learn. After all, babies are the grandmasters on this subject. In the same time that it has taken me to incrementally advance my knowledge of some tiny corner of mathematics, my children have moved from a total inability to do anything besides scream, crap themselves, and scream again, to being able to feed themselves (messily, so messily, but still), crawl, clap, grab, wave, recognise people, stand, and so on. And these are just the most visible manifestations of a deep mental transformation during which their brains have learnt huge amounts about processing sensory data and coordinating muscle movement.
If that rate of learning was to continue through their lives, they would grow into geniuses far surpassing anything humanity has seen so far. So how do they do it? Of course a large part of the answer is physiological: babies’ brains are a lot more plastic than adults’, highly efficient sponges for the absorption of new skills. There’s not a great deal we can do about that (although there may be something). All the same, I think we might be able to see some other, useful principles in action too:
- Play. We don’t usually talk about babies “working” – but they are, just as assuredly as a student revising or a scientist researching. The difference is that babies are also undeniably playing – and we wouldn’t usually describe either of the other two in that way. Babies are not motivated by exam grades or pressure to publish. The more fun you find your work, the better you do it.
- Be curious. The babies immediately home in on any new item which appears in their playing area, and start investigating. They are always exploring the room’s boundaries, and grabbing at anything unfamiliar or interesting (my laptop, mugs of hot tea, etc..). But they are not searching for anything in particular. Set aside some time for open-ended exploration and experimentation.
- First, learn one thing well. The boys learned to clap quite early on. With this under their belt, other manual skills such as waving and pointing were comparatively easy to pick up. Likewise, an experienced mathematician will find it easier than a novice to master an unfamiliar mathematical topic. Even if neither has any directly relevant knowledge, the fact that one is practised in the art of learning mathematics should carry them a long way. Building skills can be worthwhile, even when the skills themselves are not.
- A change is as good as a rest. In the opposite direction, the twins do not spend hours at a stretch practising one thing, such as walking. Instead they do it for a little bit, then get distracted by a toy, move onto another toy, have a crawling race, try holding a conversation with their mother, then they do some more walking, and so it goes on. Have more than one project on the go.
- Don’t be scared. Most of the time, my sons appear completely fearless. They happily crawl into perilous situations, pull over heavy objects, and invite disaster in any number of imaginative ways. This is despite the fact that they regularly do fall down and otherwise upset themselves. Take risks. Even if they don’t immediately pay off, continue to take risks.
- Don’t be embarrassed. Babies are not only unworried about taking a tumble, they’re also unafraid of looking like fools. The more I ponder this, the more important I think it is. In my efforts to learn Japanese, for example, I am hindered (perhaps more than I have realised) by the fear of making embarrassing mistakes in conversation with my in-laws. Likewise, mathematicians do not enjoy admitting errors, or gaps in their knowledge, in front of their colleagues (let alone their students). I think this is a bad habit. In order to learn from your mistakes, you must first allow yourself to make some.
- Accept help. The boys are utterly dependent my wife, me, and the other generous people who help us look after them (thank you!). Obviously, adults shouldn’t be that reliant on others, except in extremis. Nevertheless, there may be people in your life who would like to help you succeed. Let them.
- “Good enough” isn’t good enough. My children have reached the point where crawling is a highly efficient form of travel – they can zoom around the house to wherever they want to be. Walking, meanwhile, is a faltering, risky business. It would be a perfectly rational short term decision if they opted not to bother with it. Of course, babies don’t reason that way, which is just as well. Invest in your long-term skills, even at short term cost.
- Don’t focus on the scale of the challenge. My children’s vocabulary currently consists of little more than “dadadada”, “mamamama”, “aaaaghh”, and “pmmpphh”. It will be quite a journey from these noises to mastery of the language of Shakespeare (and indeed that of Chikamatsu). Of course they have no idea about that. The journey matters more then the destination.
I have recently been going through my book Maths 1001 making updates for a forthcoming foreign edition (of which more in future). So I have been looking over mathematical developments since approximately 2009. Thus, I present ten major developments in the subject since around then, arranged arbitrarily in ascending order of top-ness.
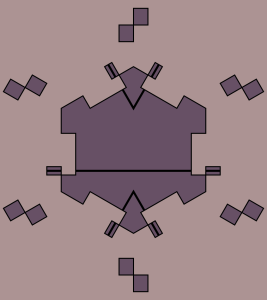
“Socolar-Taylor tile” by Parcly Taxel – Own work. Licensed under CC BY-SA 4.0 via Wikimedia Commons – https://commons.wikimedia.org/wiki/File:Socolar-Taylor_tile.svg#/media/File:Socolar-Taylor_tile.svg
10. Mochizuki’s claimed proof of the abc conjecture. The countdown kicks off on an awkward note. If Shinichi Mochizuki’s 2012 claimed proof of the abc conjecture had gained widespread acceptance, it would definitely top this list. As it is, it remains in limbo, to the enormous frustration of everyone involved.
9. The weak Goldbach conjecture. “From 7 onwards, every odd number is the sum of three primes.” We have known since 1937 that this holds for all large enough odd numbers, but in 2013 Harald Helfgott brought the threshold down to 1030, and separately with David Platt checked odd numbers up to that limit by computer.
8. Ngô Bảo Châu’s proof of the Fundamental Lemma. Bending the rules to scrape in (time-wise) is this 2009 proof of a terrifyingly technical but highly important plank of the Langlands Program.
7. Seventeen Sudoku Clues. In 2012, McGuire, Tugemann, and Civario proved that the smallest number of clues which uniquely determine a Sudoku puzzle is 17. (Although not every collection of 17 clues yields a unique solution, their theorem establishes that there can never be a valid Sudoku puzzle with only 16 clues.)
6. The Growth of Univalent Foundations/ Homotopy Type Theory. This new approach to the foundations of mathematics, led by Vladimir Voevodsky, is attracting huge attention. Apart from its inherent mathematical appeal, it promises to recast swathes of higher mathematics in a language more accessible to computerised proof-assistants.
5. Untriangulatable spaces. In sixth position is the stunning discovery, by Ciprian Manolescu, of untriangilatable manifolds in all dimensions from 5 upwards.
4. The Socolar–Taylor tile. Penrose tiles, famously, are sets of tiles which can tile the plane, but only aperiodically. It was an open question, for many years, whether it is possible to achieve the same effect with just one tile. Then Joan Taylor and Joshua Socolar found one (pictured above).
3. Completion of the Flyspeck project. In 1998, Thomas Hales announced a proof of the classic Kepler conjecture on the most efficient way to stack cannon-balls. Unfortunately, his proof was so long and computationally involved that the referees assigned to verify it couldn’t complete the task. So Hales and his team set about it themselves, using the Isabelle and HOL Light computational proof assistants. The result is not only a milestone in discrete geometry, but also in automated reasoning.
2. Partition numbers. In how many ways can a positive integer be written as a sum of smaller integers? In 2011, Ken Ono and Jan Bruinier provided the long-sought answer.
1. Bounded gaps between primes. It’s no real surprise to find that the top spot is taken by Yitang Zhang’s wonderful 2013 result that there is some number n, below 70 million, such that there are infinitely many pairs of consecutive primes exactly n apart. The subsequent flurry of activity saw James Maynard, and a Polymath Project organised by Terence Tao, bring the bound down to 246.
But, but,…?!
Where’s Hairer’s work on the KPZ equation? What about Friedman’s new examples of concrete incompleteness?! What can I say? It’s just for fun, folks. If you think I’ve got it horribly wrong, then feel free to compile your own lists. (The real answer for such things being left out is that I couldn’t easily update my book to include them.) And now…
Bonus feature! Progress in computational verifications and searches
In no particular order:
- The simple continued fraction of π has now been computed to the first 15 billion terms by Eric Weisstein, up from 100 million.
- The decimal expansion of π has been computed to 13.3 trillion digits, up from 2.69999999 trillion.
- The search for the perfect cuboid: if one exists, one of its sides must be at least 3 trillion units long, up from 9 billion.
- Goldbach’s conjecture has been verified for even numbers up to 4 × 1018 by Oliveira e Silva, up from 1018.
- The largest known twin primes are the pair either side of 3756801695685 × 2666669, up from 2003663613 × 2195000.
- The largest known prime, and the 48th known Mersenne prime (up from 47), is 257885161-1, up from 243112609-1.
- The Encyclopedia of Triangle Centres contains 7719 entries (up from 3587).
- The longest known Optimal Golomb Ruler is now 27 notches long (up from 26):
(0, 3, 15, 41, 66, 95, 97, 106, 142, 152, 220, 221, 225, 242, 295, 330, 338, 354, 382, 388, 402, 415, 486, 504, 523, 546, 553)
- The most impressive feat of integer-factorisation using classical computers, is that of the 232-digit number RSA-768:
1230186684530117755130494958384962720772853569595334792197322452 1517264005072636575187452021997864693899564749427740638459251925 5732630345373154826850791702612214291346167042921431160222124047 9274737794080665351419597459856902143413
into two 116 digit primes
3347807169895689878604416984821269081770479498371376856891243138 8982883793878002287614711652531743087737814467999489
and
3674604366679959042824463379962795263227915816434308764267603228 3815739666511279233373417143396810270092798736308917.(The previous record was the 200 digit semiprime RSA-200.)
- The most impressive feat of integer-factorisation using a quantum computer is that of 56,153=233 × 241. The previous record was 15.
- The Collatz Conjecture has been verified for numbers beyond 2 × 1021. The previous record was 5.76 × 1018. (However, this has happened via a patchwork of distributed computing projects, and I have not been able to establish with any certainty that every number up to the new higher limit has been checked. I encourage someone in this community to organise all the results in a single location.)


